Historische Cipher (Caesar Cipher bis Rot13)
Historische Chipher und deren Funktionsweise
Der grundlegende Überbegriff zu all den in den kommenden Abschnitten beschriebenen Chiffren sind die Substitutionschiffren. Substitutionschiffren verschlüsseln einen Klartext, indem sie jeden Buchstaben oder jedes Symbol im Klartext, gemäß den Anweisungen des Schlüssels und desjenigen Chiffre durch ein anderes Symbol ersetzen. Der Empfänger der Nachricht kann dann mit Hilfe des Chiffre und des passenden Schlüssels diese Substitutionen wieder rückgängig machen und erhält somit den originalen Klartext. Der Schlüssel zum Ver- und Entschlüsseln muss sowohl dem Sender als auch dem Empfänger bekannt sein. “Rotations Cipher“ und “Shiftcipher“ sind im Umkehrschluss auch Arten von Substitutionschiffren. Ganz im Gegensatz dazu gibt es noch eine zweite Kategorie an Chiffren, die Transpositionschiffren, bei welchen die Einheiten des Klartextes in einer anderen und meist recht komplexen Reihenfolge neu angeordnet werden. Die einzelnen Buchstaben bzw. Symbole selbst bleiben aber unverändert.
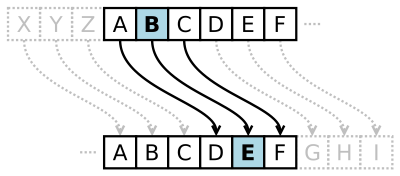
Caesar Cipher
Einer der ersten Substitutionschiffren (oder auch Shift-Chiffre) war der Caesar-Chiffre (Caesar Cipher). Hierbei werden alle Buchstaben der zu übertragenden Nachricht einzeln um drei Positionen im Alphabet verschoben (siehe Bild rechts). Der Empfänger der Nachricht vollzieht dann den umgekehrten Vorgang und verschiebt die Buchstaben um 3 Stellen zurück, um die ursprüngliche Nachricht zu erhalten. Bei dem Caesar-Chiffre handelt es sich um einen monoalphabetischen Substitutionsalgorithmus, da nur ein einziges Schlüsselalphabet verwendet wird.
Rot-N/Rot13
Erweiterte Varianten des Caesar-Chiffre findet sich in den ROT-N-Chiffren. Rot steht hierbei für “rotate“ und N für die Anzahl an Stellen um die verschoben werden soll - geschlossen übersetzt also “Rotate by N“. Ein besonderer Anwendungsfall von Rot-N ist die Rot13 Verschlüsselung. Hierbei wird ein jedes Zeichen um genau 13 Stellen im Alphabet nach hinten verschoben. Daraus ergibt sich, dass, wie in der Tabelle (Chiffrier-Tabelle zu Rot13) aufgezeigt, unter anderem ein ‘A‘ zu einem ‘N‘, ein ‘B‘ zu einem ‘O‘ und ein ‘Z‘ zu einem ‘M‘ wird.
Die Besonderheit hinter dem Rot13 Algorithmus ist, dass das Verschlüsseln und Entschlüsseln mit dem selben Schlüssel absolut ident funktionieren. Da unser Alphabet aus genau 26 Buchstaben besteht, wird aus einem jeden Buchstaben nach 2-facher Anwendung der Verschiebung um 13 Stellen im Alphabet, wieder der Ausgangs-Buchstabe. Beispielsweise wird aus einem ‘A‘ nach einmaliger Anwendung von Rot13 ein ‘N‘, aus welchem wiederum nach erneutem Einsatz wieder das ‘A‘ wird. Darüber hinaus gibt es auch noch weitere Varianten, welche dieselben Eigenschaften besitzen. Unter anderem Rot18, hierbei werden zu den 26 Buchstaben auch noch die Ziffern 0-9 hinzugezogen bzw. die Variante Rot47, welche auf den ASCII Zeichen 33-126 basiert.
Geschichte
Die Geschichte hinter dem Caesar-Chiffre (Caesar Cipher) begann, wie schon der Name verrät, mit Julius Caesar. Bevor Nachrichten verschlüsselt wurden, war es notwendig, dass Nachrichten geheim und ohne dass ein potentieller Feind an die Nachricht gelangen konnte, übermittelt werden. Rund um 100 v. Chr. entwickelt, wurde der Caesar-Cipher von Julius Caesar verwendet, um geheime Nachrichten an seine Generäle im Feld zu senden. Für den Fall, dass eine seiner Nachrichten abgefangen wurde, konnte sein Gegner sie nicht lesen. Dies verschaffte ihm einen großen strategischen Vorteil. Seine militärischen Taktiken waren dadurch unübertroffen und er stieg schließlich zum Diktator seines Reiches auf. Aber auch in seinen privaten Korrespondenzen verwendete er Chiffren. Seither sind derartige Chiffren, Weiterentwicklungen dieser Chiffren und verschlüsselte Botschaften unverzichtbare militärische Werkzeuge. Zusammenfassend ist der Caesar-Cipher ein klassisches und auch eines der ersten dokumentierten Beispiele antiker Kryptographie.
Erweiterungen des Caesar Cipher
Vigenère Cipher
Das Vigenère Cipher ist ein klassische Chipher und verwendet eine einfache Form der polyalphabetischen Substitution. Eine polyalphabetische Chiffre ist eine Chiffre, welche auf der einfachen Substitution basiert und mehrere Substitutionsalphabete verwendet. Die Verschlüsselung des Originaltextes erfolgt mit dem Vigenère-Quadrat oder der Vigenère-Tabelle. Die Tabelle besteht aus den Alphabeten, die 26 Mal in verschiedenen Reihen ausgeschrieben sind, wobei jedes Alphabet im Vergleich zum vorherigen Alphabet zyklisch nach links verschoben ist. Dies entspricht wiederum den 26 möglichen Caesar-Chiffren. Das an jedem Punkt verwendete Alphabet hängt von einem sich wiederholenden Schlüsselwort ab, welches vorab zwischen Sender und Empfänger ausgetauscht werden muss. Beim Vigenère Cipher wird also die Verschiebung der Buchstaben nicht um eine fixe Anzahl an Stellen (wie beim Caesar Cipher) bestimmt, sondern durch ein Schlüsselwort.
Mathematisch ausgedrückt bedeutet das, wenn man einem jeden Buchstaben seine Position als Ziffer zuweist (0-25), dass zu demjenigen Ausgangsbuchstaben, der dazugehörige Buchstabe aus dem Schlüssel addiert wird. Das Ergebnis muss wieder an das Alphabet (0-25) angepasst werden.
C = (P + K) mod 26 C = Ciphertext / P = Plaintext / K = Key
Die Entschlüsselung erfolgt, indem man zu der Zeile in der Tabelle geht, die dem Schlüssel entspricht, die Position des Chiffretext-Buchstabens in dieser Zeile finden und dann den Buchstaben der Spalte für den Klartext verwenden. Mathematisch sieht das ganze wie folgt aus:
P = (E − K + 26) mod 26 C = Ciphertext / P = Plaintext / K = Key
Playfair Cipher
Ein weiterer symmetrischer, monoalphabetischer Substitutionalgorithmus ist der Playfair Cipher, welcher 1854 vom britischen Wissenschaftler Charles Wheatstone Playfair erfunden wurde. Lange Zeit galt der Playfair-Algorithmus als sicheres Verschlüsselungsverfahren. Seine Verschlüsselungsideen sind in Bezug auf Netzwerksicherheit und Datenverschlüsselung weit verbreitet. Der Playfair Cipher ist ein Verschlüsselungsalgorithmus, der zweibuchstabige Silben im Klartext als Einheit verwendet und in Chiffretext umwandelt. Der ursprüngliche Algorithmus kann 26 ¨ ×26 Buchstabenpaare verwenden, obwohl er eine etwas flachere Häufigkeitsverteilungskurve als Klartext hat.
Für die Verschlüsselung wird eine 5x5 Tabelle benötige, welche mit dem Schlüssel befüllt wird und in weiterer Folge als Schlüssel zur Verschlüsselung dient. Weitere leere Felder werden mit dem Alphabet in alphabetischer Reihenfolge aufgefüllt. Wichtig ist dabei, dass jeder Buchstabe immer nur einmal vorkommen darf. Danach wird der Klartext in Paare von immer 2 Buchstaben, sogenannte Digraphen, getrennt. Ist die Anzahl der Buchstaben ungerade oder sind in einem Digraphen 2 gleiche Buchstaben werden weitere Buchstaben hinzugefugt. Um die Digraphen zu verschlüsseln gibt es 3 Methoden.
- Wenn die beiden Buchstaben in derselben Zeile der 5x5 Tabelle stehen, wird jeder Buchstabe zu dem ihm rechtsstehenden Buchstaben.
- Wenn die beiden Buchstaben in derselben Spalte der 5x5 Tabelle stehen, wird jeder Buchstabe zu dem von ihm aus darunterstehenden Buchstaben.
- Trifft keiner der beiden Fällt zu, wird ein Rechteck mit 2 weiteren Buchstaben geformt. Es wird der Buchstabe aus dem Klartext zu dem horizontalen Gegenüber aus dem Rechteck.
Danach werden die Digraphen wieder zusammengesetzt und das Ergebnis ist der verschlüsselte Text.
Aktuelle Anwendungsfälle in Kryptosystemen
Substitutions-Chiffren, wie oben beschrieben, insbesondere die älteren Chiffren, werden nicht mehr ernsthaft verwendet. Grundlegend kann der Ceasar Cipher und weiterführend auch der Vigenère Cipher oder der Playfair Cipher auf keinen Fall als sicher angesehen werden. Der Vigenère Cipher wird zwar mit zunehmender Länge der Schlüssels immer sicherer, allerdings bieten auch längere Schlüssel aufgrund der einfachen Methodik zu wenig Schutz. Aufgrund dessen finden sie auch kaum Verwendung in den Verschlüsselungsalgorithmen von heute. Für derartige Algorithmen ist die Rechenleistung von aktuellen Computer- und Server-Systemen viel zu hoch und sie können in wenigen Sekunden von sogar einfachen Client-Systemen ausgehebelt werden.
Heutzutage werden derartige Chiffren nur noch von Lehrern als Programmieraufgabe, als einfache offensichtliche Verschlüsselungsmethoden im Internet oder in Capture-the-flag Aufgaben im Bereich der Cybersecurity verwendet.
Anwendungsgebiete von ROT13 sind beispielsweise UNIX-Betriebssystemen, Internetforen und Rätsel (damit die Lösung nicht auf den ersten Blick ersichtlich ist).
Das kryptografische Konzept der Substitution setzt sich jedoch trotzdem bis heute fort. Aus einer ausreichend abstrakten Perspektive können moderne bitorientierte Blockchiffren als Substitutions-Chiffren auf einem enorm großen binären Alphabet angesehen werden. Manche dieser arbeiten, wie auch unter anderem der Vigenère Cipher, mit sogenannten Substitutions-Permutations-Netzwerken (SP Netzwerke) bzw. mit Substitutions-Boxen (S-Boxen). Beispiele dazu sind unter anderem der AES (Advanced Encryption Standard), welcher auch mit erwähnten SP-Netzwerken arbeitet oder der DES (Data Encryption Standard), welcher wiederum mit S-Boxen arbeitet.
Kryptoanalysen/Angriffe
Brute-Force
Brute-Force-Angriffe behandeln das Ausprobieren aller möglichen Zeichenkombinationen, um den "Schlüssel“ zum Entschlüsseln einer verschlüsselten Nachricht zu finden. Während Brute-Force-Angriffe bei kleineren Schlüsselräumen weniger Zeit in Anspruch nehmen, dauert es bei größeren Schlüsselräumen erheblich länger.
Im Falle des Ceasar Ciphers ist die Anzahl der verschiedenen Schlüssel auf 26 begrenzt (alle Werte zwischen 0 und 25), sodass ein trivialer Brute-Force-Angriff machbar ist. Im Gegensatz dazu beträgt bei dem Vigenère Cipher die Anzahl der möglichen Schlüssel 26^x, also alle möglichen Folgen von Buchstaben der Länge x. Für x, die groß genug sind, verhindert dies Brute-Force-Angriffe.
Frequency Analysis (Häufigkeitsanalyse)
Die Frequency Analysis ist eine der bekanntesten Chiffretext-Angriffe. Sie basiert auf der Untersuchung der Häufigkeit von Zeichen oder einer Gruppe von Zeichen in einem Geheimtext. In jeder Sprache werden nicht alle Zeichen gleich häufig verwendet. Für jeden Sprachprozentsatz des Vorhandenseins aller Zeichen, die signifikant unterschiedlich sind, hat der in der Sprache geschriebene Text mehrere bestimmte gemeinsame Eigenschaften, die es ihnen ermöglichen, sich von Texten zu unterscheiden, die in anderen Sprachen geschrieben sind. Betrachten wir die englische Sprache sind ”E“, ”T“,”A“ und ”O“ die am häufigsten vorkommenden Buchstaben, wahrend Buchstaben wie ”Z“, ”Q“ und ”X“ am seltensten vorkommen.
Der grundlegende Ansatz der Häufigkeitsanalyse besteht darin, zuerst die Häufigkeit von Geheimtextbuchstaben zu zählen und ihnen dann erratene Klartextbuchstaben zuzuordnen. Kommt ein Buchstabe im Chiffretext öfter vor als alle anderen deutet das darauf hin, dass dieser Buchstabe im Klartext ”E“ entspricht. ”T“ und ”A“ sind im Englischen auch sehr verbreitet, und könnten somit auch für den Geheimtextbuchstaben in Frage kommen. Daher muss der Kryptoanalytiker möglicherweise mehrere Kombinationen von Zuordnungen zwischen Geheimtext- und Klartextbuchstaben ausprobieren. Somit kann mit dieser Methode, bei einer Anwendung auf z.B. den Ceasar Cipher, sehr schnell der angewandte Schlüssel gefunden werden. Der Playfair-Cipher ist wiederum deutlich schwieriger aufzulösen. Der Hauptgrund besteht daran, dass im Gegensatz zu den im Ceasar Cipher 25 möglichen Monographien, bei dem Playfair-Cipher 25*25 und somit 625 möglichen Digraphen gibt, mit welchen der Klartext verschlüsselt worden sein könnte.
Weitere Kryptoanalysen
Neben der Analyse von Buchstabenhäufigkeiten lassen sich auch andere Muster, auch ”Pattern” genannt, erkennen, die bei der Entschlüsselung eines Geheimtextes helfen. Aufbauend auf diesen Pattern können ganze Worte aus dem Geheimtext in Klartext umgewandelt werden und in weiterer Folge der komplette Text entschlüsselt werden.
In der heutigen Zeit wird der Großteil der Arbeit an Kryptoanalysen von Computern erledigt. Weiterführend wird auch an der Möglichkeit gearbeitet, neuronale Netze zu trainieren, um verschlüsselte Nachrichten mit unbekanntem geheimen Schlüssel zu entschlüsseln. Die Netzwerke werden trainiert, indem Daten in einer Form bereitgestellt werden, welche die Schwachstelle zusammen mit dem Verschlüsselungsschlüssel aufzeigt, bis das Netzwerk in der Lage ist, den Schlüssel (oder seine Wahrscheinlichkeit) für jeden möglichen Chiffretext zu verallgemeinern und vorherzusagen (oder seine Wahrscheinlichkeit abzuschätzen). Mit anderen Worten, neuronale Netze werden für den Kryptoanalytiker zu einem Werkzeug, um seine Angriffe zu automatisieren und zu optimieren. Der Kryptoanalytiker weist auf die Schwachstelle hin und das neuronale Netz lernt, wie es sie ausnutzt.
References
- Mohammed Al-Amin and Abdulrahman Olaniyan. Vigenere cipher: Trends review and possible modifications. In International Journal of Computer Applications 135, volume 5, pages 46–50, February 2016.
- Aakash, Soni Jitendra Kumar, and Sharma Bharti. A. j. cipher. In 2017 2nd International Conference on Telecommunication and Networks (TELNET), pages 1–6, 2017
- Bhat Bawna, Ali AbdulWahid, and Gupta Apurva. Des and aes performance evaluation. In International Conference on Computing, Communication Automation, pages 887–890, 2015
- Robert Churchhouse. Codes and ciphers: Julius caesar, the enigma and the internet. In Cambridge University Press, 2002
- Riccardo Focardi and Flaminia L. Luccio. Neural cryptanalysis of classical ciphers. In https://ceur-ws.org/Vol-2243/paper10.pdf [Online] Zugriff am: 4.11.2022.
- L. C. Han and N. M. Mahyuddin. An implementation of caesar cipher and xor encryption technique in a secure wireless communication. In 2014 2nd International Conference on Electronic Design (ICED), volume 6, pages 111–116, 2014.
- K. Prasanthi K. Senthil and R. Rajaram. A modern avatar of julius ceasar and vigenere cipher. In 2013 IEEE International Conference on Computational Intelligence and Computing Research, volume 3, pages 1–3, 2013.
- T. Mantoro and Y. Lazuardi. Sms based home appliance security approach using rot 13, rc4 and rsa algorithm. In 2017 International Conference on Computing, Engineering, and Design (ICCED), volume 5, pages 1–5, 2017.
- Victor Ruzhentsev, Roman Levchenko, and Oleksandr Fediushyn. Cryptanalysis of simple substitution-permutation cipher using artificial neural network. In 2020 IEEE International Conference on Problems of Infocommunications. Science and Technology (PIC ST), 2020.
- J. Sanchez, R. Correa, H. Buena, S. Arias, and H. Gomez. Encryption techniques: A theoretical overview and future proposals. In Third International Conference on eDemocracy eGovernment, volume 5, pages 60–64, March 2016.
- Nikhil Sharma, Himmat Meghwal, Munish Mehta, and Tarun Kumar. A review on playfair substitution cipher and frequency analysis attack on playfair. In 2018 2nd International Conference on Trends in Electronics and Informatics (ICOEI), 2018
- Timothy J. Shimeall and Jonathan M. Spring. Introduction to information security a strategic-based approach. 2014
- Yuzhe Wang. A classical cipher-playfair cipher and its improved versions. In 2021 International Conference on Electronic Information Engineering and Computer Science (EIECS), pages 123–126, 2021
- Jean-Philippe Aumasson. Serious Cryptography: A Practical Introduction to Modern Encryption. No Starch Press, USA, 2017.
- Reni Rahmadani, Bagoes Maulana, Muhammad Dominique Mendoza, Andreas Pratama Partogu Hutabarat, and Larson Carstein Raja Aritonang. Combination of rot13 cryptographic algorithm and ecb (electronic codebook) in data security. EAI, 2023.


