Elliptic Curve Cryptography

Summary

This documentary gives a brief introduction into elliptic curve cryptography

Elliptic Curve Cryptography (ECC)

Elliptic curve cryptography is a part of asymmetric cryptography, it is based on the mathematical hard problem to find a solution for the elliptic curve discrete logarithm. The calculations are performed on the algebraic structure of elliptic curves over finite fields, which means we compute points on a elliptic curve over finite field by applying the group operations double and add. The scalar multiplication of a point on an elliptic curve over a finite field is equivalent to the exponentation of a number in a prime field, therefore the inversion is also called discrete logarithm. First proposed application of elliptic curves in cryptography was random number generations, now ECC is widely used for key establishment and digital signature schemes. The main advantage of ECC is that it offers the same security level compared to RSA with shorter key lengths. Efficient implementations make ECC usable for constraint devices enabling security and privacy protection for emerging IoT systems.

Example usage of ECC in IoT:

ZigBee Smart Energy(1.x and 1.2)	sect163k1(1.x), sect283k1(1.2)
Vehicular Ad-Hoc Networks (IEEE1609.2)	secp224r1,secp256r1
NFC Forum Signature Record Type Definition(RTD)	sec192r1, secp224r1, sect233k1, sect233r1

Simple Weierstrass Elliptic Curve Presentation

• Simple Weierstrass form curve equation:

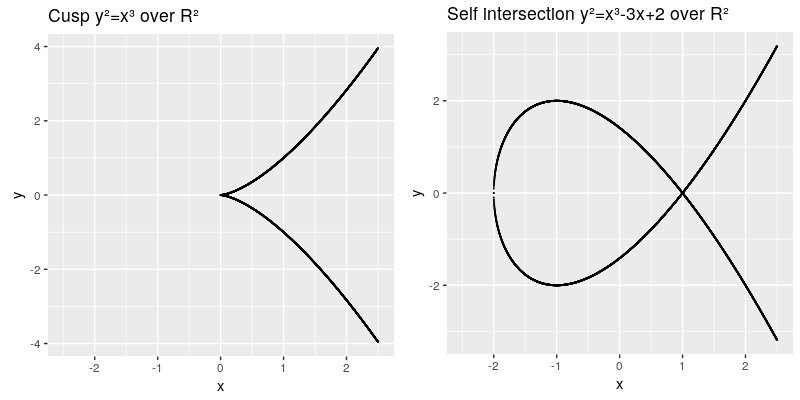
$y^{2}=x^{3}+ax+b$ The elliptic curve are all points in the $x,y$ coordinates $P(x,y)$ which fulfill the cubic curve equation, whereas $a$ and $b$ are called the characteristic of the curve. The curve needs to be smooth, which means that it will not contain any singularities such as a cusp or a self intersection,

This can be also described by the term: $4a^{3}+27b^{2}\neq 0$

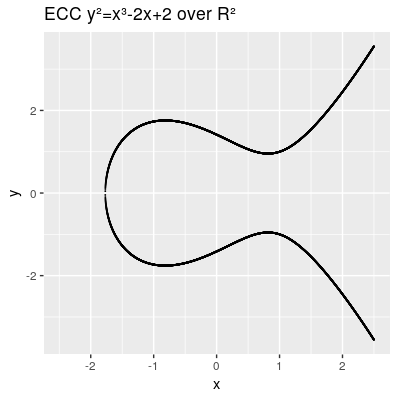
Another characteristic we need to introduce is the point at infinity denoted by ${\mathcal {O}}$ (also known as ideal point), which can be thought as identity element infinitly raised on the y axis. Therefore our points on the elliptic curve over R² all fulfill this equation $\{(x,y)\in R^{2}|y^{2}=x^{3}+ax+b,4a^{3}+27b^{2}\neq 0\}\cup \{{\mathcal {O}}\}$. A valid curve over rational numbers is shown in the next image.

In cryptography elliptic curves over finite fields are used. The number of rational points $\#E$ of an elliptic curve over a finite field $K$ e.g. the prime field $GF(p)$ can be computed with the Schoof-Elkies-Alkin algorithm, which is implemented in the PARI/GP library. The Hasse theorem gives an estimation of the number of points in the intervall:

$p+1-2{\sqrt {p}}\leq \#E\leq p+1+2{\sqrt {p}}$

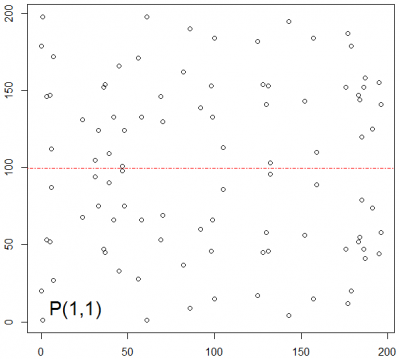
The next figure shows a elliptic cuve $E:y^{2}=x^{3}-2x+2$ over a finite field, the prime field GF(199). On each y-axis are two points, the point and its inverse point, mapped into the positive space of the prime field.

Group Operations on Elliptic Curves

According to the group law all points support following operations:

• Point Addition: $P+Q=R$
• Case $Q=P$ -> Point Doubling: $2P=R$
• Case $Q=-P$ -> Inversion of a Point: $P+(-P)={\mathcal {O}}$

Point Addition

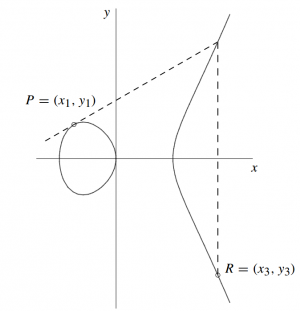
Given the elliptic curve $E:y^{2}=x^{3}+ax+b$ and the points $P=(x_{1},y_{1})$ and $Q=(x_{2},y_{2})$, we can calculate the coordinates of the point $R(x_{3},y_{3})$ by adding this two points $R=P+Q$ as follows.

Geometric derivation of the Point Addition by the Tangent Chord Law

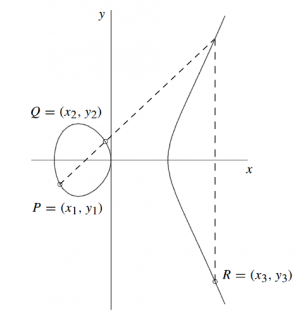
In the geometric derivation a line/chord is drawn through $P$ and $Q$, the result point R is the symmtric inversion on the $y$ axis of the point at the 3rd intersection on the elliptic curve. 1. Calculation of the equation of the chord

• We know the equation from the line

$y=kx+d\qquad {\text{concizing of}}\qquad k={\frac {\Delta y}{\Delta x}}$

• Therefore

$k={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}$ and we can find the intersection with the y-axis and achieve d $d=y_{1}-kx_{1}={\frac {y_{1}\cdot x_{2}-y_{1}\cdot x_{1}-y_{2}\cdot x_{1}+y_{1}\cdot x_{1}}{x_{2}-x_{1}}}={\frac {y_{1}\cdot x_{2}-y_{2}\cdot x_{1}}{x_{2}-x_{1}}}$.

2. Calculation of $y_{3}$ $y_{3}$ we can find by insertion in the line equation:

$y_{3}=(-1){\bigg (}{\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}\cdot x_{3}+y_{1}-{\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}\cdot x_{1}{\bigg )}={\bigg (}{\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}{\bigg )}(x_{1}-x_{3})-y_{1}$

2. Calculation of $x_{3}$

• In the intersection point of the chord with the tangent, the $y$ coordinate satisfies both equations, therefore we can extract $y$ from both equations and get a new equation.

${\begin{aligned}(k\cdot x+d)^{2}&=x^{3}+a\cdot x+b\\k^{2}x^{2}+2k\cdot x\cdot d+d^{2}&=x^{3}+a\cdot x+b\\x^{3}-x^{2}k^{2}+x(a-2k\cdot d)+b-d^{2}&=0\end{aligned}}$

• This is a equation of 3rd degree therefore we have 3 cross points, which can be searched by

${\begin{aligned}(x-x_{1})\cdot (x-x_{2})\cdot (x-x_{3})&=0\\(x^{2}-x\cdot x_{2}-x\cdot x_{1}+x_{1}\cdot x_{2})\cdot (x-x_{3})&=0\\x^{3}-x^{2}\cdot x_{2}-x^{2}\cdot x_{1}+x\cdot x_{1}x_{2}-x^{2}\cdot x_{3}+x\cdot x_{2}x_{3}+x\cdot x_{1}x_{3}-x_{1}x_{2}x_{3}&=0\\x^{3}-x^{2}(x_{1}+x_{2}+x_{3})+x(x_{1}x_{2}+x_{2}x_{3}+x_{1}x_{3})+x_{1}x_{2}x_{3}&=0\end{aligned}}$

• Now we can conclude from the second term

${\begin{aligned}x^{3}-x^{2}{\underline {k^{2}}}+x(a-2k\cdot d)+b-d^{2}&=0\\x^{3}-x^{2}{\underline {(x_{1}+x_{2}+x_{3})}}+x(x_{1}x_{2}+x_{2}x_{3}+x_{1}x_{3})+x_{1}x_{2}x_{3}&=0\\k^{2}&=x_{1}+x_{2}+x_{3}\end{aligned}}$

• and achieve a solution for $x_{3}$ by:

$x_{3}=k^{2}-x_{1}-x_{2}={\bigg (}{\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}{\bigg )}^{2}-x_{1}-x_{2}$

$x_{3}={\bigg (}{\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}{\bigg )}^{2}-x_{1}-x_{2}\ {\text{ and }}\ y_{3}={\bigg (}{\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}{\bigg )}(x_{1}-x_{3})-y_{1}{\text{ over }}E$

This operation is also called the Point Addition in affine coordinates and the computational costs are 1 x inversion, 2 x multiplications and 1 x squaring. Interactive tool to visualize point addition.

Point Doubling

Given the elliptic curve $E:y^{2}=x^{3}+ax+b$ and the special case $P=Q$ with the point $P=(x_{1},y_{1})$. The result point $R(x_{3},y_{3})$ is achieved by doubling the point $R=2P$ as follows.

Geometric derivation of the Point Doubling by the Tangent Chord Law

For the doubling a tangent is drawn at point $P$. At the intersection with the elliptic curve again the inversion on the $y$ is taken to achieve the result point $R$.

1. The tangent in point $P$ has the equation of $y=kx+d$. The slope of the tangent $k$ is calculated by the differential function of $E$ by $\delta x$ and $\delta y$.

$k={\frac {E\delta x}{E\delta y}}={\frac {(y^{2}=x^{3}+ax+b)\delta x}{(y^{2}=x^{3}+ax+b)\delta y}}={\frac {3x_{1}^{2}+a}{2y_{1}}}$

and then the intersection of the tangent with the y-axis is calculated by inserting the point coordinates $P(x_{1},y_{1})$ in the equation of the tangent $y=kx+d$.

$d=y_{1}-k\cdot x_{1}=y_{1}-{\frac {3x_{1}^{2}+a}{2y_{1}}}\cdot x_{1}$

2. The y-coordinate of the point of the second intersection with the elliptic curve $y_{3}$ can be calculated by inserting the point coordinates in the equation of the tangent and multiply by $(-1)$ to get the inverse point on the y axis.

$y_{3}=(-1)(kx_{3}+d)=(-1){\bigg (}{\frac {3x_{1}^{2}+a}{2y_{1}}}\cdot x_{3}+y_{1}-{\frac {3x_{1}^{2}+a}{2y_{1}}}\cdot x_{1}{\bigg )}={\bigg (}{\frac {3x_{1}^{2}+a}{2y_{1}}}{\bigg )}(x_{1}-x_{3})-y_{1}$

3. $y_{3}$ is achieved by inserting

${\begin{aligned}(k\cdot x+d)^{2}&=x^{3}+a\cdot x+b\\k^{2}x^{2}+2k\cdot x\cdot d+d^{2}&=x^{3}+a\cdot x+b\\x^{3}-x^{2}k^{2}+x(a-2k\cdot d)+b-d^{2}&=0\end{aligned}}$

• The crossing points can be searched by

${\begin{aligned}(x-x_{1})^{2}\cdot (x-x_{3})&=0\\(x^{2}-2x\cdot x_{1}+x_{1}^{2})\cdot (x-x_{3})&=0\\x^{3}-2x^{2}\cdot x_{1}+x\cdot x_{1}^{2}-x^{2}\cdot x_{3}+2x\cdot x_{1}x_{3}-x_{1}^{2}x_{3}&=0\\x^{3}-x^{2}(2x_{1}+x_{3})+x(x^{2}+(x_{1}x_{3})^{2})+x_{1}^{2}x_{3}&=0\end{aligned}}$

• Now we can conclude from the second term

${\begin{aligned}x^{3}-x^{2}{\underline {k^{2}}}+x(a-2k\cdot d)+b-d^{2}&=0\\x^{3}-x^{2}{\underline {(2x_{1}+x_{3})}}+x(x_{1}^{2}-2x_{1}x_{3})+x_{1}^{2}x_{3}&=0\\k^{2}&=2x_{1}+x_{3}\end{aligned}}$

• and achieve a solution for $x_{3}$ by:

$x_{3}=k^{2}-2x_{1}={\bigg (}{\frac {3x_{1}^{2}+a}{2y_{1}}}{\bigg )}^{2}-2x_{1}={\bigg (}{\frac {3x_{1}^{2}+a}{2y_{1}}}{\bigg )}^{2}-2\cdot x_{1}$

$y_{3}={\bigg (}{\frac {3x_{1}^{2}+a}{2y_{1}}}{\bigg )}(x_{1}-x_{3})-y_{1}\ {\text{ and }}\ x_{3}={\bigg (}{\frac {3x_{1}^{2}+a}{2y_{1}}}{\bigg )}^{2}-2\cdot x_{1}\ {\text{ over }}E$

This operation is also called the Point Doubling in affine coordinates and the computational costs are 1 x inversion, 2 x multiplications and 2 x squarings.

Example of elliptic point operations over an elliptic curve over a finite field

Given a curve E $E:y^{2}=x^{3}+3x+5{\text{ over }}\mathbb {Z} _{17}$ we examine the basic operations on the elliptic curve:

• Validation of the elliptic curve: This is done to determine if the elliptic curve is smooth by calculating the discriminant.

$\Delta =-16(4a^{3}+27b^{2})=-12528\equiv 1(\mod 17)$ therefore $\Delta \neq 0$ holds and this curve can be used for EC operations.

• Examining the number of points: Choosing one random point of the curve P(6,1) as generator G all points on the curve can be calculated with the equations given above over a the prime field 17. This means first the point gets doubled and a modulo 17 operation is applied. Then continuously all other points are calculated by adding the point P to the result each time applying the modulo 17 .

(6,1)	(4,8)	(15,5)	(9,9)	(11,14)	(2,6)	(1,14)	(12,1)
(16,16)	(10,10)	(5,14)	(5,3)	(10,7)	(16,1)	(12,16)	(1,3)
(2,11)	(11,3)	(9,8)	(15,12)	(4,9)	(6,16)	${\mathcal {O}}$

All by point P(6,1) generated 23 points satisfy the equation of the elliptic curve. Notice that each x value has two y values.

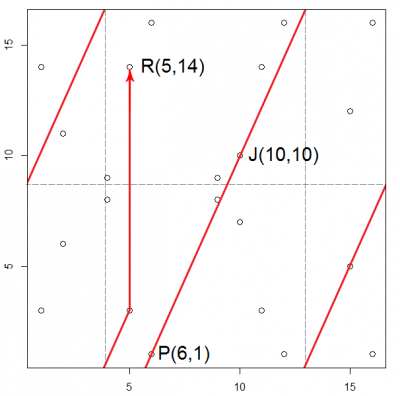
• Point Addition:$P(6,1)+J(10,10)=?$

The points P(6,1) and J(10,10) are added with calculations in the finite field using the modular operation each time. ${\begin{aligned}m&={\bigg (}{\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}{\bigg )}\mod 17=(10-1)\cdot (10-6)^{-1}\mod 17\\&=9\cdot 4^{-1}\mod 17=9\cdot 13\mod 17\\&=117\mod 17=15\\\end{aligned}}$

$x_{3}=m^{2}-x_{1}-x_{2}\mod 17=15^{2}-6-10\mod 17=4-6-10\mod 17=-12\mod 17=5$

$y_{3}=m(x_{1}-x_{3})-y_{1}=15(6-5)-1\mod 17=14$

Solution: $P(6,1)+J(10,10)=R(5,14)$ The addition of point P and J to get the result point R is visualized in the next figure.

Algebraic group properties of the points

The points further comply associative and commutative algebraic group laws and the handling of the neutral element:

• Closure: $P+Q=R\quad \forall \quad P,Q,R\in E$
• Associative law: $P+{\mathcal {O}}={\mathcal {O}}+P\quad \forall \quad P\in E$
• Identity element and inverse that: $P+(-P)={\mathcal {O}}\quad \forall \quad P\in E$
• Cummutative law: $P+(Q+R)=(P+Q)+R\quad \forall \quad P,Q,R\in E$

The inverse point of a point P(x,y) is therefore P(x,-y).

Scalar Multiplication

Is the mainly used operation on elliptic curves in cryptography, it adds $n$ times the point $P$ of the elliptic curve over a finite field e.g. prime field $GF(p)$.

$nP=\underbrace {P+P+P+P+...+P} _{\text{n times}}\ text{over}E$

Standardization of elliptic curves

The domain parameters for ECC schemes are described in the form $E(q,a,b,G,n,h)$.

Parameter description
$q$	defines the field size, either a prime $p$ or $2^{m}$ where m is prime
$a$	first parameter of the curve equation
$b$	second parameter of the curve equation
$G$	generating point consisting of both point coordinates $(x_{G},y_{G})$
$n$	order of the point $G$
$h$	cofactor which is equal to the order of the curve divided by $n$

The generation of safe elliptic curves is an effort, hence it is recommended to use standardized known curves. First curves have been standardized in the ANSI X9.62 standard by the American National Standards Institute(ANSI) in 1999 , these have been extended or replaced by ANSI X9.63 in 2001 and ANSI FRP256V1 in 2011. The National Institute of Standard and Technology (NIST) defined their own curves in the NIST FIPS 186-2 in 2000. In the same year the Certicom published the widely-used Certicom SEC2 curves which have been continously updated in version 2 . In 2005 NIST published the NSA Suite B and the Federal Office for Information Security in Germany proposed their own randomly generated curves in the same year.

Curve25519

Curve25519 is a highly optimized curve proposed by Daniel J. Bernstein (djb) in 2005 . The curve equation is

$y^{2}=x^{3}+486662x^{2}+x$ over a prime field $2^{255}-19$

Edward curves

Applications of Elliptic Curve Cryptography

Example: Elliptic Curve Diffie Hellman Key Exchange (ECDH)

Is a key establishment protocol that allows two parties which know the common domain parameter of a curve $E(p,a,b,G,n,h)$ to calculate a common shared secret over an insecure channel. Assuming Alice and Bob like to establish a common shard secret for communication, both need to generate a keypair. A keypair consists of a private/secret key $d_{i}$ and a public key $Q_{i}$ . For the private key $d_{i}$ a integer less than $n$ is randomly selected, then both need to calculate their public key with $Q_{i}=d_{i}\cdot G$, so that Alice has a pair of $(d_{A},Q_{A})$. She sends her public key $Q_{A}$ to Bob and he sends back his public key $Q_{B}$. Now both are able to calculate the shared secret, Alice computes $K_{AB}=Q_{B}\cdot d_{A}$ and Bob $K_{BA}=Q_{A}\cdot d_{B}$. This works because $K_{AB}=Q_{B}\cdot d_{A}=(d_{B}\cdot G)\cdot d_{A}=(d_{A}\cdot G)\cdot d_{B}=K_{BA}$.

Online resources

• https://safecurves.cr.yp.to/
• https://andrea.corbellini.name/2015/05/17/elliptic-curve-cryptography-a-gentle-introduction/
• https://www.allaboutcircuits.com/technical-articles/elliptic-curve-cryptography-in-embedded-systems/