Difference between revisions of "Elliptic Curve Cryptography"
(Created page with "== Elliptic Curve Cryptography == == Summary == This documentary gives a brief introduction into elliptic curve cryptography ==Elliptic Curve Cryptography == Elliptic cu...") |
|||
| Line 15: | Line 15: | ||
==Simple Weierstrass Elliptic Curve Presentation== | |||
< | * Simple Weierstrass form curve equation: | ||
<math>y² = x³ + ax + b</math> | |||
a | The elliptic curve are all points in the x,y coordinates which fulfill the cubic curve equation, whereas a and b are called the characteristic of the curve. | ||
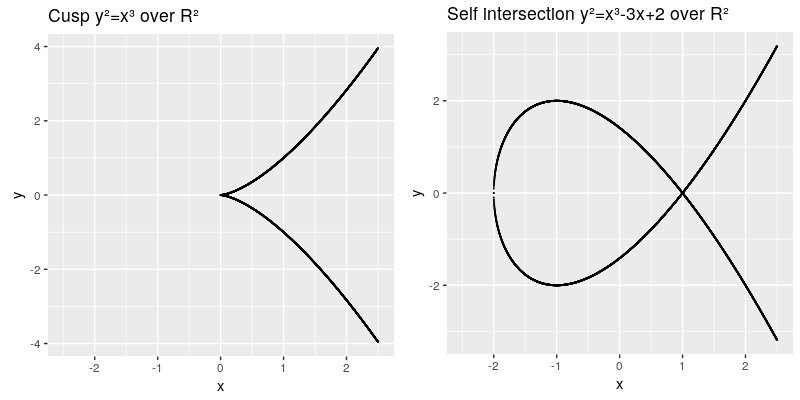
The curve needs to be smooth, which means that it will not contain any singularities such as a cusp or a self intersection, | |||
[[File:Singularities.png]] | |||
This can be also described by the term: | |||
<math>4a^3 + 27b^2 \neq 0</math> | |||
Another characteristic we need to introduce is the point at infinity denoted by 0 (also known as ideal point), which can be thought as identity element infinitly raised on the y axis. | |||
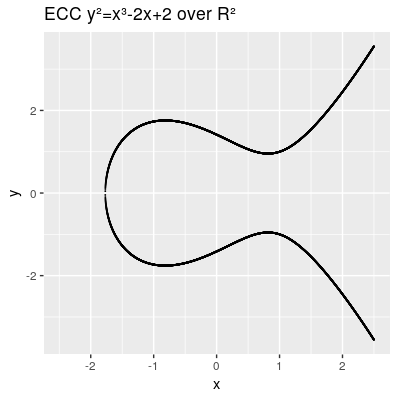
Therefore our points on the elliptic curve over R² all fulfill this equation | |||
<math>\{(x,y)∈R2 | y2=x3+ax+b, 4a3+27b2≠0\} \cup \{0\}</math> | |||
and can be presented by: | |||
[[File:Ecc.png]] | |||
[[Category:Basic]] | [[Category:Basic]] | ||
Revision as of 20:52, 9 February 2019
Elliptic Curve Cryptography
Summary
This documentary gives a brief introduction into elliptic curve cryptography
Elliptic Curve Cryptography
Elliptic curve cryptography is a part of asymmetric cryptography, it is based on the mathematical hard problem to find a solution for the elliptic curve discrete logarithm. The calculations are performed on the algebraic structure of elliptic curves over finite fields, which means we compute points on a elliptic curve over finite field by applying the group operations double and add.
The scalar multiplication of a point on an elliptic curve over a finite field is equivalent to the exponentation of a number in a prime field, therefore the inversion is also called discrete logarithm.
First proposed application of elliptic curves in cryptography was random number generations, now ECC is widely used for key establishment and digital signature schemes.
Simple Weierstrass Elliptic Curve Presentation
- Simple Weierstrass form curve equation:
Failed to parse (syntax error): {\displaystyle y² = x³ + ax + b} The elliptic curve are all points in the x,y coordinates which fulfill the cubic curve equation, whereas a and b are called the characteristic of the curve. The curve needs to be smooth, which means that it will not contain any singularities such as a cusp or a self intersection,
This can be also described by the term:
Another characteristic we need to introduce is the point at infinity denoted by 0 (also known as ideal point), which can be thought as identity element infinitly raised on the y axis. Therefore our points on the elliptic curve over R² all fulfill this equation Failed to parse (syntax error): {\displaystyle \{(x,y)∈R2 | y2=x3+ax+b, 4a3+27b2≠0\} \cup \{0\}} and can be presented by: