Elliptic Curve Cryptography

Summary

This documentary gives a brief introduction into elliptic curve cryptography

Elliptic Curve Cryptography

Elliptic curve cryptography is a part of asymmetric cryptography, it is based on the mathematical hard problem to find a solution for the elliptic curve discrete logarithm. The calculations are performed on the algebraic structure of elliptic curves over finite fields, which means we compute points on a elliptic curve over finite field by applying the group operations double and add.

The scalar multiplication of a point on an elliptic curve over a finite field is equivalent to the exponentation of a number in a prime field, therefore the inversion is also called discrete logarithm.

First proposed application of elliptic curves in cryptography was random number generations, now ECC is widely used for key establishment and digital signature schemes.

Simple Weierstrass Elliptic Curve Presentation

• Simple Weierstrass form curve equation:

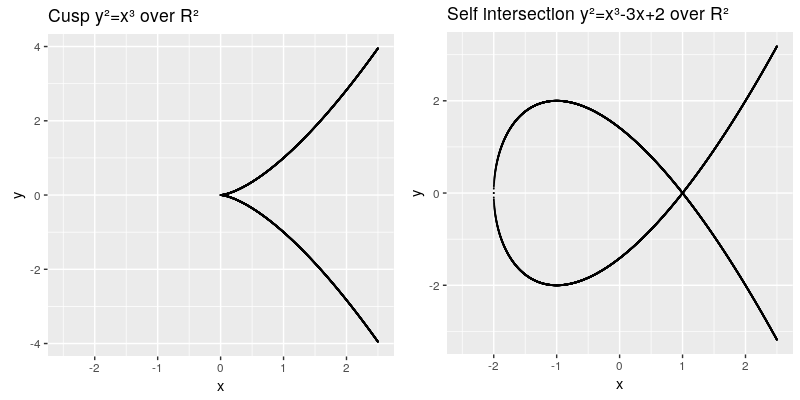
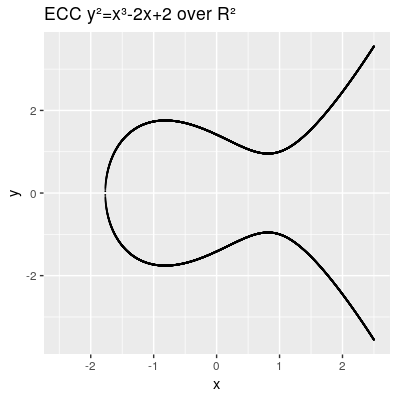
TODO need to install math extension: https://www.mediawiki.org/wiki/Extension:Math/advancedSettings#Installing_texvc Failed to parse (syntax error): {\displaystyle y² = x³ + ax + b} The elliptic curve are all points in the x,y coordinates which fulfill the cubic curve equation, whereas a and b are called the characteristic of the curve. The curve needs to be smooth, which means that it will not contain any singularities such as a cusp or a self intersection,

This can be also described by the term: $4a^{3}+27b^{2}\neq 0$

Another characteristic we need to introduce is the point at infinity denoted by 0 (also known as ideal point), which can be thought as identity element infinitly raised on the y axis. Therefore our points on the elliptic curve over R² all fulfill this equation Failed to parse (syntax error): {\displaystyle \{(x,y)∈R2 | y2=x3+ax+b, 4a3+27b2≠0\} \cup \{0\}} and can be presented by:

A point consists of 2 values P(x,y).

Group operations on elliptic curves

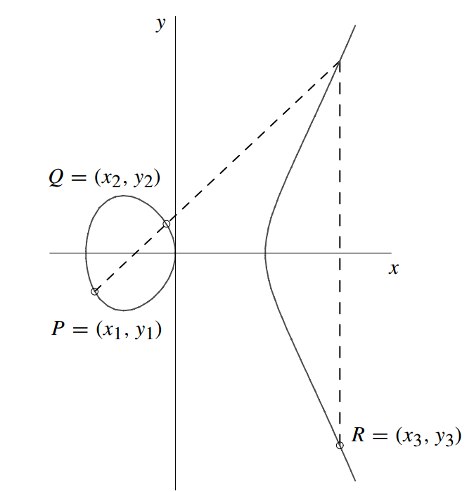
According to the group law all points support following operations:

• Point addition: $P+Q=R$
• Point doubling: <math> P=Q - 2P=R<\math

TODO:Need to install link target extension: https://www.mediawiki.org/wiki/Extension:LinkTarget Test: https://cdn.rawgit.com/andreacorbellini/ecc/920b29a/interactive/reals-add.html

Geometric derivation of the point addition by the Tangent Chord Law

TODO: Need to install Cite extension: https://www.mediawiki.org/wiki/Extension:Cite