Elliptic Curve Cryptography

Summary

This documentary gives a brief introduction into elliptic curve cryptography

Elliptic Curve Cryptography

Elliptic curve cryptography is a part of asymmetric cryptography, it is based on the mathematical hard problem to find a solution for the elliptic curve discrete logarithm. The calculations are performed on the algebraic structure of elliptic curves over finite fields, which means we compute points on a elliptic curve over finite field by applying the group operations double and add. The scalar multiplication of a point on an elliptic curve over a finite field is equivalent to the exponentation of a number in a prime field, therefore the inversion is also called discrete logarithm.

First proposed application of elliptic curves in cryptography was random number generations, now ECC is widely used for key establishment and digital signature schemes.

Simple Weierstrass Elliptic Curve Presentation

• Simple Weierstrass form curve equation:

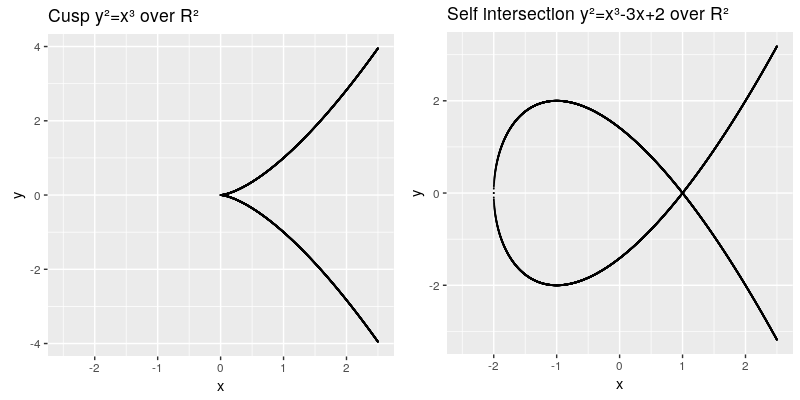
$y^{2}=x^{3}+ax+b$ The elliptic curve are all points in the $x,y$ coordinates $P(x,y)$ which fulfill the cubic curve equation, whereas a and b are called the characteristic of the curve. The curve needs to be smooth, which means that it will not contain any singularities such as a cusp or a self intersection,

This can be also described by the term: $4a^{3}+27b^{2}\neq 0$

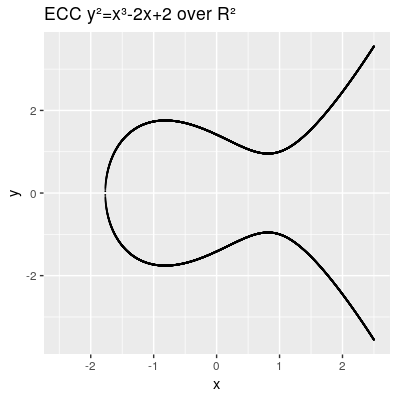
Another characteristic we need to introduce is the point at infinity denoted by ${\mathcal {O}}$ (also known as ideal point), which can be thought as identity element infinitly raised on the y axis. Therefore our points on the elliptic curve over R² all fulfill this equation $\{(x,y)\in R^{2}|y^{2}=x^{3}+ax+b,4a^{3}+27b^{2}\neq 0\}\cup \{{\mathcal {O}}\}$. A valid curve is shown in the next image.

Group Operations on Elliptic Curves

According to the group law all points support following operations:

• Point Addition: $P+Q=R$
• Case: $Q=P$ -> Point Doubling : $2P=R$
• Case: $Q=-P$ -> Inversion of a Point: $P+(-P)={\mathcal {O}}$

TODO:Need to install link target extension: https://www.mediawiki.org/wiki/Extension:LinkTarget

Point Addition

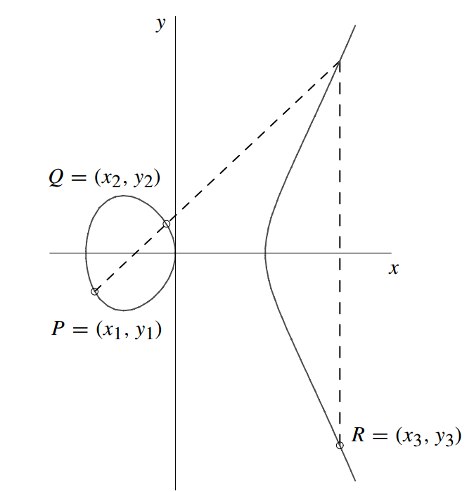
Given the elliptic curve $E:y^{2}=x^{3}+ax+b$ and the points $P=(x_{1},y_{1})$ and $Q=(x_{2},y_{2})$, we can caculate the coordinates of the point $R=P+Q=(x_{3},y_{3})$ as follows.

Geometric derivation of the point addition by the Tangent Chord Law

1. Calculation of $y_{3}$

• We know the equation from the line

$y=kx+d\qquad {\text{concising of}}\qquad k={\frac {\Delta y}{\Delta x}}$

• Therfore

$k={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}$ and we can find the intersection with the y-axis and achieve d $d=y_{1}-kx_{1}={\frac {y_{1}\cdot x_{2}-y_{1}\cdot x_{1}-y_{2}\cdot x_{1}+y_{1}\cdot x_{1}}{x_{2}-x_{1}}}={\frac {y_{1}\cdot x_{2}-y_{2}\cdot x_{1}}{x_{2}-x_{1}}}$.

• $y_{3}$ we can find by insertion in the line equation:

$y_{3}=(-1){\bigg (}{\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}\cdot x_{3}+y_{1}-{\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}\cdot x_{1}{\bigg )}={\bigg (}{\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}{\bigg )}(x_{1}-x_{3})-y_{1}$

2. Calculation of $x_{3}$

• Now we insert the values of the line equation into the elliptic curve equation:

${\begin{aligned}(k\cdot x+d)^{2}&=x^{3}+a\cdot x+b\\k^{2}x^{2}+2k\cdot x\cdot d+d^{2}&=x^{3}+a\cdot x+b\\x^{3}-x^{2}k^{2}+x(a-2k\cdot d)+b-d^{2}&=0\end{aligned}}$

• The cross points can be searched by

${\begin{aligned}(x-x_{1})\cdot (x-x_{2})\cdot (x-x_{3})&=0\\(x^{2}-x\cdot x_{2}-x\cdot x_{1}+x_{1}\cdot x_{2})\cdot (x-x_{3})&=0\\x^{3}-x^{2}\cdot x_{2}-x^{2}\cdot x_{1}+x\cdot x_{1}x_{2}-x^{2}\cdot x_{3}+x\cdot x_{2}x_{3}+x\cdot x_{1}x_{3}-x_{1}x_{2}x_{3}&=0\\x^{3}-x^{2}(x_{1}+x_{2}+x_{3})+x(x_{1}x_{2}+x_{2}x_{3}+x_{1}x_{3})+x_{1}x_{2}x_{3}&=0\end{aligned}}$

• Now we can conclude from the second term

${\begin{aligned}x^{3}-x^{2}{\underline {k^{2}}}+x(a-2k\cdot d)+b-d^{2}&=0\\x^{3}-x^{2}{\underline {(x_{1}+x_{2}+x_{3})}}+x(x_{1}x_{2}+x_{2}x_{3}+x_{1}x_{3})+x_{1}x_{2}x_{3}&=0\\k^{2}&=x_{1}+x_{2}+x_{3}\end{aligned}}$

• and achieve a solution for $x_{3}$ by:

$x_{3}=k^{2}-x_{1}-x_{2}={\bigg (}{\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}{\bigg )}^{2}-x_{1}-x_{2}$

This is also called the calculations in affine coordinates and the computational costs are 1 x inversion, 2 x multiplications and 1 x quadration. Interactive tool to visualize point addition online at https://cdn.rawgit.com/andreacorbellini/ecc/920b29a/interactive/reals-add.html. The Point Addition over an elliptic curve over a finite field (e.g. prime field) is shown in the next image.

Algebraic group of points

The points further comply associative and commutative algebraic group laws and the handling of the neutral element:

• Closure: $P+Q=R\quad \forall \quad P,Q,R\in E$
• Associative law: $P+{\mathcal {O}}={\mathcal {O}}+P\quad \forall \quad P\in E$
• Identity element and inverse that: $P+(-P)={\mathcal {O}}\quad \forall \quad P\in E$
• Cummutative law: $P+(Q+R)=(P+Q)+R\quad \forall \quad P,Q,R\in E$

The inverse point of a point P(x,y) is therefore P(x,-y).

Scalar Multiplication

Is main used operation in cryptography, it adds n times the point P of the elliptic curve over a prime field.

$nP=\underbrace {P+P+P+P+...+P} _{\text{n times}}$

Standardization of elliptic curves

The domain parameters for ECC schemes are described in the form $E(q,a,b,G,n,h)$.

Parameter description
$q$	defines the field size, either a prime $p$ or $2^{m}$ where m is prime
$a$	first parameter of the curve equation
$b$	second parameter of the curve equation
$G$	generating point consisting of both point coordinates $(x_{G},y_{G})$
$n$	order of the point $G$
$h$	cofactor which is equalto the order of the curve divided by $n$

The generation of safe elliptic curves is an effort, hence it is recommended to use standardized known curves. First curves have been standardized in the ANSI X9.62 standard by the American National Standards Institute(ANSI) in 1999 , these have been extended or replaced by ANSI X9.63 in 2001 and ANSI FRP256V1 in 2011. The National Institute of Standard and Technology (NIST) defined their own curves in the NIST FIPS 186-2 in 2000. In the same year the Certicom published the widely-used Certicom SEC2 curves which have been continously updated in version 2 . In 2005 NIST published the NSA Suite B and the Federal Office for Information Security in Germany proposed their own randomly generated curves in the same year.

Curve25519

Curve25519 is a highly optimized curve proposed by Daniel J. Bernstein (djb) in 2005. The curve equation is $y^{2}=x^{3}+486662x^{2}+x$ over a prime field $2^{255}-19$

Applications of Elliptic Curve Cryptography

Example Elliptic Curve Diffie Hellman Key Exchange (ECDH)

Is a key establishment protocol that allows two parties which know the parameter of a curve $E(p,a,b,G,n,h)$ to calculate a common shared secret over an insecure channel.

Online resources

https://safecurves.cr.yp.to/ https://andrea.corbellini.name/2015/05/17/elliptic-curve-cryptography-a-gentle-introduction/